Sorting and Searching - CSES Problem Set Solutions
I solved all problems on this page without any hints/spoilers (not even reading the CSES recommended book).
Visit https://cses.fi/problemset/ for the full problem set.
I don't provide the full problem specifications on this page due to possible copyright issues. Links to the original problem specs are provided below along with the date accessed, which should allow you to use Internet Archive if the original URL hosting a problem specification ever meaningfully changes.
Distinct Numbers [Spec] (2024-01-15)
#!/usr/bin/env python3
input()
nums = input().strip().split()
print(len(set(nums)))Apartments [Spec] (2024-01-15)
My approach starts by making the applicants and apartments arrays each into sorted stacks (the top is the biggest). We then compare the current biggest apartment with the current applicant with the biggest desired size:
- If the apartment is too big, then we know the apartment will never be filled since the current biggest applicant doesn’t want it. We pop it from the apartment stack.
- Otherwise, if the apartment is too small, then we know the applicant will never get an apartment since the current biggest apartment is too small. We pop that applicant from the applicant stack.
- Otherwise, we know that the applicant can fill the apartment, so we pop both the applicant and apartment from their stacks and we increment our current count of filled apartments.
Full solution:
#!/usr/bin/env python3
(_, _, k) = [int(x) for x in input().strip().split()]
desired_sizes = sorted(int(x) for x in input().strip().split())
apt_sizes = sorted(int(x) for x in input().strip().split())
solution = 0
while len(desired_sizes) and len(apt_sizes):
if apt_sizes[-1] > desired_sizes[-1] + k:
apt_sizes.pop()
elif apt_sizes[-1] < desired_sizes[-1] - k:
desired_sizes.pop()
else:
solution += 1
apt_sizes.pop()
desired_sizes.pop()
print(solution)Ferris Wheel [Spec] (2024-01-16)
#!/usr/bin/env python3
from collections import deque
(_, max_weight) = [int(x) for x in input().strip().split()]
dq = deque(sorted(int(x) for x in input().strip().split()))
gondolas = 0
while len(dq) > 1:
gondolas += 1
if dq[0] + dq[-1] <= max_weight:
dq.popleft()
dq.pop()
print(gondolas + (len(dq) > 0))Concert Tickets [Spec] (2024-01-18)
I initially misunderstood the problem spec and thought that there was no time dimension to the problem, leading to two totally incorrect solutions:
#!/usr/bin/env python3
input()
tickets = sorted(int(x) for x in input().strip().split())
bids = sorted(int(x) for x in input().strip().split())
for bid in reversed(bids):
while len(tickets) and (tickets[-1] > bid):
tickets.pop()
if len(tickets):
print(tickets.pop())
else:
print(-1)#!/usr/bin/env python3
input()
tickets = sorted(int(x) for x in input().strip().split())
bids = sorted((int(x), i) for i, x in enumerate(input().strip().split()))
results = [None]*len(bids)
for bid, i in reversed(bids):
while len(tickets) and (tickets[-1] > bid):
tickets.pop()
results[i] = tickets.pop() if len(tickets) else -1
print("\n".join(str(x) for x in results))The first logically correct solution I made was too slow due to element deletions (even when I submitted it for PyPy3), leading to an overall time complexity is . I would’ve liked to use a BST data structure like C++‘s std::multiset, but Python lacks a standard library implementation.
#!/usr/bin/env python3
from bisect import bisect_right
input()
tickets = sorted(int(x) for x in input().strip().split())
bids = [int(x) for x in input().strip().split()]
for bid in bids:
i = bisect_right(tickets, bid)
if i == 0:
print(-1)
else:
print(tickets.pop(i - 1))
But at least I know the idea works, leading me to my first successful solution that passed all tests. I decided to rewrite in C++ since I wasn’t having any luck in Python. This solution has time complexity due to operations on std::multiset, sorting, and main loop:
#include <algorithm>
#include <iostream>
#include <set>
#include <vector>
int main() {
int n, m;
std::cin >> n >> m;
std::multiset<long> tickets;
std::vector<long> bids;
for (int i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
tickets.insert(-tmp);
}
for (int i = 0; i < m; ++i) {
long tmp;
std::cin >> tmp;
bids.push_back(tmp);
}
for (auto bid : bids) {
const auto i = tickets.lower_bound(-bid);
if (i == tickets.end()) {
std::cout << -1 << std::endl;
} else {
std::cout << -(*i) << std::endl;
tickets.erase(i);
}
}
return 0;
}I decided to see if I can still make Python work without too much effort. I could probably try to paste a BST implementation, but I’d rather not.
I used union find to let me skip over “deleted” tickets efficiently rather than carry out deletions. My solution passes on both CPython3 and PyPy3:
#!/usr/bin/env python3
from bisect import bisect_right
input()
tickets = sorted(int(x) for x in input().strip().split())
bids = [int(x) for x in input().strip().split()]
skips = list(range(len(tickets)))
def canonical(i):
if i < 0:
return i
elif i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
for bid in bids:
i = canonical(bisect_right(tickets, bid) - 1)
if i == -1:
print(-1)
else:
print(tickets[i])
skips[i] = canonical(i - 1)Restaurant Customers [Spec] (2024-01-19)
I initially attempted Python, but TLE’d with PyPy3:
#!/usr/bin/env python3
from sys import stdin
from itertools import chain
stdin.readline()
customers = [[int(t) for t in s.strip().split()] for s in stdin.readlines()]
(cur_t, cur_cust, prev_max) = (0, 0, 0)
for t, v in sorted(chain(((x, 1) for x, _ in customers), ((x, -1) for _, x in customers))):
if t != cur_t:
prev_max = max(cur_cust, prev_max)
cur_t = t
cur_cust += v
print(max(cur_cust, prev_max))#!/usr/bin/env python3
from sys import stdin
from collections import Counter
stdin.readline()
customers = [[int(t) for t in s.strip().split()] for s in stdin.readlines()]
difs = Counter(t for t, _ in customers)
difs.subtract(t for _, t in customers)
difs = sorted(difs.items())
(cur, solution) = (0, 0)
for _, v in difs:
cur += v
solution = max(cur, solution)
print(solution)#!/usr/bin/env python3
from sys import stdin
from itertools import accumulate
from collections import Counter
from operator import add
stdin.readline()
customers = [[int(t) for t in s.strip().split()] for s in stdin.readlines()]
difs = Counter(t for t, _ in customers)
difs.subtract(t for _, t in customers)
difs = sorted(difs.items())
print(max(accumulate((v for _, v in difs), add)))Switching over to C++ and reimplementing my first Python solution passed all tests:
#include <iostream>
#include <vector>
int main() {
long n;
std::cin >> n;
std::vector<std::pair<long, int>> difs;
for (long i = 0; i < n; ++i) {
long start, end;
std::cin >> start >> end;
difs.emplace_back(start, 1);
difs.emplace_back(end, -1);
}
std::sort(difs.begin(), difs.end());
long cur_t = 0;
long cur_cust = 0;
long prev_max = 0;
for (auto [t, v] : difs) {
if (t != cur_t) {
prev_max = std::max(prev_max, cur_cust);
cur_t = t;
}
cur_cust += v;
}
std::cout << std::max(prev_max, cur_cust) << std::endl;
return 0;
}TODO: Maybe try to get a Python solution to pass!
TODO: Someone on Discord got a very normal-looking non-cursed Python solution working, so it’s definitely very possible in Python! They suggested that instead of sorting a 2*n-sized list, you could just have two n-sized lists. Maybe that will help things?
Movie Festival [Spec] (2024-01-19)
I went straight to C++ due to my experience with Python TLE’ing Restaurant Customers:
#include <iostream>
#include <vector>
int main() {
long n;
std::cin >> n;
std::vector<std::pair<long, long>> intervals;
for (long i = 0; i < n; ++i) {
long start, end;
std::cin >> start >> end;
intervals.emplace_back(start, end);
}
std::sort(intervals.begin(), intervals.end());
long solution = 0;
long prev_b = 0;
for (auto [a, b] : intervals) {
if (a >= prev_b) {
// Guaranteed to add a new movie
prev_b = b;
++solution;
} else if (b >= prev_b) {
// Offers no advantages to the previous one
continue;
} else {
// We prefer to take this film instead of the previous one
prev_b = b;
}
}
std::cout << solution << std::endl;
return 0;
}As it turns out, my C++ solution wouldn’t have to take advantage of BSTs, so I did a quick Python rewrite. It passes CPython3, but somehow TLE’s with PyPy3:
#!/usr/bin/env python3
from sys import stdin
stdin.readline()
intervals = sorted([int(x) for x in s.strip().split()] for s in stdin.readlines())
(prev_b, solution) = (0, 0)
for (a, b) in intervals:
if a >= prev_b:
prev_b = b
solution += 1
elif b < prev_b:
prev_b = b
print(solution)Sum of Two Values [Spec] (2024-01-20)
Two different approaches came to mind immediately: two-pointer, or dictionary.
I went for the dictionary approach first, but it TLE’d on both CPython3 and PyPy3:
#!/usr/bin/env python3
from collections import defaultdict
(_, x) = [int(s) for s in input().strip().split()]
arr = [(int(s), i) for i, s in enumerate(input().strip().split())]
buckets = defaultdict(list)
for v, i in arr:
buckets[v].append(i + 1) # i+1 because one-indexed for some reason
def run():
for v in buckets.keys():
other = x - v
if other == v:
if len(buckets[v]) > 1:
return f"{buckets[v][0]} {buckets[v][1]}"
elif other in buckets:
return f"{buckets[v][0]} {buckets[other][0]}"
return "IMPOSSIBLE"
print(run())Redoing it with a two-pointer approach passed all tests for CPython3:
#!/usr/bin/env python3
from collections import defaultdict
(_, x) = [int(s) for s in input().strip().split()]
arr = sorted((int(s), i + 1) for i, s in enumerate(input().strip().split()))
# i+1 because it's 1-indexed for some reason
(lo, hi) = (0, len(arr) - 1)
while (hi > lo) and (arr[hi][0] + arr[lo][0] != x):
if arr[hi][0] + arr[lo][0] > x:
hi -= 1
else:
lo += 1
print(f"{arr[lo][1]} {arr[hi][1]}" if (hi > lo) else "IMPOSSIBLE")In retrospect, I should’ve started with the two-pointer approach. It turned out much simpler to work through.
Maximum Subarray Sum [Spec] (2024-01-22)
#!/usr/bin/env python3
input()
arr = [int(s) for s in input().strip().split()]
(solution, cur_sum, min_sum) = (arr[0], 0, 0)
for v in arr:
cur_sum += v
solution = max(solution, cur_sum - min_sum)
min_sum = min(min_sum, cur_sum)
print(solution)Stick Lengths [Spec] (2024-01-23)
This one took an embarrassing amount of time for me to figure out.
I started off with an incorrect solution of taking the average stick length and finding the cost of bringing all sticks to the average length:
#!/usr/bin/env python3
input()
sticks = [int(s) for s in input().strip().split()]
avg = sum(sticks) // len(sticks)
print(sum(abs(stick - avg) for stick in sticks))I mistakenly thought maybe it was a rounding error with finding the average since I used floor/integer division. In an attempt to solve this, I took the best solution of the floored average and floored average plus 1. This also produced incorrect answers:
#!/usr/bin/env python3
input()
sticks = [int(s) for s in input().strip().split()]
avg = sum(sticks) // len(sticks)
print(min(
sum(abs(stick - avg) for stick in sticks),
sum(abs(stick - avg - 1) for stick in sticks),
))The next idea I tried was to sort the sticks and use a two-pointer approach.
The first key insight in working through a two-pointer solution was that I didn’t need to worry about the order of the sticks, so I could sort the sticks. With a sorted array, I found that you can incrementally calculate costs. For example, consider a sorted sticks array . We can draw this with ASCII art:
H H
H H H
H H H H H
H H H H H
H H H H H H
H H H H H H
H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7 <-- indicesSuppose we want all the sticks to all be 6 units long. Sticks at indices 3 and 4 are already 6 units long, but the sticks to the left (indices 0-2) must be increased in length while the sticks to the right (indices 5-7) must have their lengths reduced:
. .
. . .
. . . H H H H H
. . . H H H H H
. . H H H H H H
. . H H H H H H
. H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7We see that the cost to make all sticks 6 units long is .
To calculate these costs incrementally, we might start by making all sticks the same length as stick 0. For purposes of this discussion, we say that we are “visiting stick 0”. The diagram for visiting stick 0:
. .
. . .
. . . . .
. . . . .
. . . . . .
. . . . . .
. . . . . . .
H H H H H H H H
0 1 2 3 4 5 6 7We also precalculate the cost of this configuration. Here, we see that the cost when visiting stick 0 is .
Now let’s visit the next stick up (stick 1). Since it’s hard to see what’s going on in the example, I will skip over explaining it. Drawing it out:
. .
. . .
. . . . .
. . . . .
. . . . . .
. . . . . .
. H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7The cost when visiting stick 1 is .
Now, this is where things get more interesting. Let’s visit the next stick up (stick 2). The diagram should now look like this:
. .
. . .
. . . . .
. . . . .
. . H H H H H H
. . H H H H H H
. H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7The cost when visiting stick 2 is .
Notice that the difference between visiting stick 1 and visiting stick 2 is “two rectangles”.
“Rectangle 1” spans sticks 0-1:
. .
. . .
. . . . .
. . . . .
[X X] H H H H H H
[X X] H H H H H H
. H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7“Rectangle 2” spans sticks 2-7:
. .
. . .
. . . . .
. . . . .
. . [X X X X X X]
. . [X X X X X X]
. H H H H H H H
H H H H H H H H
0 1 2 3 4 5 6 7The widths and heights of these rectangles simply depend on:
- the current visited stick, and
- the difference in length between the currently-visited stick and the previously-visited stick.
To calculate the cost of visiting the current stick, we can simply add the size of “rectangle 1” to the cost, and then subtract the size of “rectangle 2” from the cost:
This cost matches the cost we calculated for visiting stick 2.
This method of course generalizes across the entire sorted array of sticks.
The second key insight I made while working out how a two-pointer solution might work was that the optimal stick size will always be one of the stick sizes that already exist in the array.
To get at why this is the case, let’s consider a very simple sorted array of sticks :
H H H H
H H H H
H H H H H H
H H H H H H
H H H H H H
0 1 2 3 4 5We can roughly do two things:
- we can add length to sticks 0-1, or
- we can remove length from sticks 2-5.
Doing the first option will add 2 to the cost for every unit of length added, while doing the second option will add 4 to the cost for every unit of length removed. Clearly, the best option is to simply bring sticks 0-1 up to height 5, which incurs a total cost of 4. Note that if you “meet halfway” by bringing all sticks to length 4, you still find that cutting the length of sticks 2-5 is less-efficient than adding length to sticks 0-1.
This should be sufficient background for understanding my remaining solutions.
Unfortunately, my two-pointer idea didn’t work and gave wrong answers. The idea of the algorithm was that I would start with a sort of “visit the left pointer” and “visit the right pointer”, then I check which pointer is cheaper to move. I keep moving the pointers until they meet, and the meeting point is my solution. The issue is evidently locally suboptimal solutions which I won’t expand further on. In retrospect, I should’ve checked the edge cases better. The failed two-pointer solution:
#!/usr/bin/env python3
from itertools import accumulate, pairwise
input()
sticks = sorted(int(s) for s in input().strip().split())
(left, right) = (0, len(sticks) - 1)
(llen, rlen) = (1, 1)
cost = 0
while right > left:
(llen, rlen) = (left + 1, len(sticks) - right)
ladd = (sticks[left + 1] - sticks[left]) * llen
radd = (sticks[right] - sticks[right - 1]) * rlen
if ladd > radd:
cost += radd
right -= 1
else:
cost += ladd
left += 1
print(cost)I quickly come up with the idea to just try visiting every stick in the sorted list and getting the lowest-cost. My very first solution that passed all tests:
#!/usr/bin/env python3
from itertools import accumulate, pairwise
input()
sticks = sorted(int(s) for s in input().strip().split())
def op_left(acc, cur):
(i, (prev_v, v)) = cur
return acc + ((v - prev_v) * i)
def op_right(acc, cur):
(i, (prev_v, v)) = cur
return acc + ((prev_v - v) * i)
costsl = accumulate(
enumerate(pairwise(sticks), start=1),
op_left,
initial=0,
)
costsr = reversed(list(accumulate(
enumerate(pairwise(reversed(sticks)), start=1),
op_right,
initial=0,
)))
print(min(a + b for a, b in zip(costsl, costsr)))I also did another solution that is based around a cumulative sum array:
#!/usr/bin/env python3
from itertools import accumulate
from math import inf
input()
sticks = sorted(int(s) for s in input().strip().split())
sums = list(accumulate(sticks, initial=0))
solution = inf
for i, stick in enumerate(sticks):
left_cost = (i * stick) - sums[i]
right_cost = (sums[-1] - sums[i + 1]) - ((len(sticks) - i - 1) * stick)
solution = min(solution, left_cost + right_cost)
print(0 if (len(sticks) == 1) else solution)My favourite variant I made that uses this incremental solutions idea:
#!/usr/bin/env python3
input()
sticks = sorted(int(s) for s in input().strip().split())
cost = sum(sticks)
prev = 0
for i, stick in enumerate(sticks):
dif = (stick - prev) * ((2 * i) - len(sticks))
if dif > 0:
break # short circuit
cost += dif
prev = stick
print(cost)That solution notably uses a conditional break (“short circuit”). This works since cost behaves like a parabola when visiting each stick in a sorted stick array.
This is the point where I spoiled the answers for myself and looked at other peoples’ solutions.
After spoiling solutions, a common one I found was to simply visit the median/middle stick:
#!/usr/bin/env python3
input()
sticks = sorted(int(s) for s in input().strip().split())
print(sum(abs(stick - sticks[len(sticks) // 2]) for stick in sticks))To gain an intuition for going on here, let’s try a skewed distribution . The median is calculated as . Sketching out the diagram:
H
H H
H H H
H H H
H H H
H H H
H H H H
H H H H
H H H H H H
H H H H H H H
0 1 2 3 4 5 6
^
medianAll sticks need to be brought to the same length, so the outliers necessarily have to be dealt with anyway. The following diagram incurs a cost of :
.
. .
[H H H]
[H H H]
[H H H]
[H H H]
H [H H H]
H [H H H]
[. H H] H [H H H]
[H H H] H [H H H]
0 1 2 3 4 5 6
^I also highlighted two rectangles in the diagram above. Notice that both rectangles are the same width, therefore they will incur the same cost to modify.
The one stick that we shouldn’t touch is the median stick (stick 3) since modifying it at all will incur unnecessary cost. Therefore, stick 3’s length will be the target length for all the sticks. The cheapest cost for this distribution is to then lengthen the left rectangle by 2, and shorten the right rectangle by :
.
. .
. . .
. . .
. . .
. . .
[. . .] H [H H H]
[. . .] H [H H H]
[. H H] H [H H H]
[H H H] H [H H H]
0 1 2 3 4 5 6
^These rectangle-lengthenings and shortenings adds , so the total cost is , and this is the cheapest cost for this distribution.
But what about an even-numbered distribution? Let’s try . The median middle is calculated as . Sketching out the diagram:
H
H H
H H
H H
H H
H H
H H H
H H H
H H H H H
H H H H H H
0 1 2 3 4 5
^
middleOnce again, we deal with the outliers, this time incurring a cost of :
.
[H H]
[H H]
[H H]
[H H]
[H H]
H [H H]
H [H H]
[. H H] H [H H]
[H H H] H [H H]
0 1 2 3 4 5
^This time, the two rectangles are mismatched in width!
However, we can conceptually combine the middle stick with the rectangle with the smallest width. This is efficient because the smaller width is cheaper to modify than the wider width. This will always be the rectangle to the right. Modifying this right rectangle and thereby adding to the cost by :
.
. .
. .
. .
. .
. .
[H H H]
[H H H]
[. H H] [H H H]
[H H H] [H H H]
0 1 2 3 4 5
^
middleNow, there’s just two rectangles. Trivially, you can modify either of them and it will incur the same cost. For fun, let’s modify both of them, thereby adding to the cost by :
.
. .
. .
. .
. .
. .
. . .
[. . .] [H H H]
[. H H] [H H H]
[H H H] [H H H]
0 1 2 3 4 5
^The total cost of these operations is , and this is the cheapest cost.
Though, in practice, we’ll just keep things simple and bring everything to the same level as the middle stick, which is what that Python implementation does.
Missing Coin Sum [Spec] (2024-01-24)
This was a fun one to figure out!
I started by sorting the input array and thinking about how smaller coins have a different effect to larger coins in that they allow for “finer-grained sums”. Therefore, dealing with the smaller coins first may be a useful strategy for this problem.
My next idea was to think of intervals of consecutive integers (i.e. sequences where each element is one greater than the previous). I thought about different ideas like needing to track intervals using tuples and whether or not to start the intervals from , but here’s what I found worked.
We track a single unbroken interval of possible coin sums that starts with . The basic idea is that we incrementally grow this interval until we find a gap where a sum isn’t possible. To understand what this means, let’s look at an example.
Let’s consider a simple sorted list of four coins . Let’s conceptually initialize a set of “seen coins” called . I say conceptually because the set isn’t explicitly initialized in my Python implementation, but it will be useful for understanding it.
Before starting the loop, the set is empty:
We find that the only possible coin sum for is because is an empty set. Let’s track this with an interval we’ll call , and also sketch it out using an integer number line (with bold X representing set membership):
| X | ||||||||||
(This interval notation means an interval starting at (inclusive) and ending at (exclusive). This notation is typically used for real number intervals rather than integers, but I like borrowing the notation for integer intervals as well.)
Now, let’s start the loop.
Let’s visit the first element of the sorted coins list:
[ 1, 2, 6, 7 ]
^Therefore we add the element to the seen set:
And therefore, the set of possible coin sums is:
| X | X | |||||||||
This new interval makes sense since there are now two possible subsets of :
Let’s visit the next element:
[ 1, 2, 6, 7 ]
^Therefore we add the element to the seen set:
And therefore, the set of possible coin sums is:
| X | X | X | X | |||||||
This new interval makes sense since there are four possible subsets of , each with unique sum values:
Let’s visit the next element:
[ 1, 2, 6, 7 ]
^And now, we notice something interesting happens:
| X | X | X | X | X | X | X | X | |||
We now have a gap in what should’ve been a single unbroken interval! The algorithm terminates here, and the answer is .
My solution uses these ideas, but with many shortcuts applied:
#!/usr/bin/env python3
input()
coins = sorted(int(s) for s in input().strip().split())
interval_len = 1 # INTERVAL STARTS AT AND INCLUDES ZERO
for coin in coins:
if coin > interval_len:
break
interval_len += coin
print(interval_len)Collecting Numbers [Spec] (2024-01-26)
#!/usr/bin/env python3
input()
nums = [int(s) for s in input().strip().split()]
seen = [True] + ([False]*len(nums))
rounds = 1
for v in nums:
if not seen[v - 1]:
rounds += 1
seen[v] = True
print(rounds)Collecting Numbers II [Spec] (2024-01-27)
I took ages to get my first successful solution, and I feel like there should be a much simpler solution here. I originally went for C++ for the BST data structures, but my attempts to use BSTs didn’t work out due to the complexity of my idea of using tuple representations of range intervals (tracking the start and end of each interval). I eventually settled on just tracking the base of these range intervals.
This solution comes awfully close to TLE’ing (it took 0.88s for test 2).
TODO: There is almost certainly a better solution. I should meditate on this some more.
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
int main() {
int n, m;
std::cin >> n >> m;
std::vector<long> nums;
std::vector<std::pair<long, long>> ops;
for (int i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
nums.push_back(tmp);
}
for (int i = 0; i < m; ++i) {
long tmp1, tmp2;
std::cin >> tmp1 >> tmp2;
ops.emplace_back(tmp1 - 1, tmp2 - 1); // -1 to convert to 0-indexed
}
std::unordered_map<long, long> numsmap; // number --> index
std::unordered_set<long> bases {0, (long) nums.size() + 1};
for (std::size_t i = 0; i < nums.size(); ++i) {
if (!numsmap.contains(nums[i] - 1)) {
bases.insert(nums[i]);
}
numsmap.emplace(nums[i], i);
}
for (const auto &[a, b] : ops) {
const auto &av = nums[a];
const auto &bv = nums[b];
bases.insert(av);
bases.insert(bv);
bases.insert(av + 1);
bases.insert(bv + 1);
std::swap(nums[a], nums[b]);
std::swap(numsmap[av], numsmap[bv]);
const auto op = [&](const long &xv){
const auto &it0 = bases.find(xv);
if ((it0 != bases.end()) && (numsmap[xv - 1] < numsmap[xv])) {
bases.erase(it0);
}
const auto &it1 = bases.find(xv + 1);
if ((it1 != bases.end()) && (numsmap[xv + 1] > numsmap[xv])) {
bases.erase(it1);
}
};
op(av);
op(bv);
bases.insert(1); // Always a base
std::cout << bases.size() - 2 << std::endl; // << std::endl;
}
return 0;
}Playlist [Spec] (2024-01-27)
I went for a sliding window solution:
#!/usr/bin/env python3
input()
songs = [int(s) for s in input().strip().split()]
(lo, hi) = (0, 0)
songs_in_seq = {songs[0]}
longest_seq = 1
while hi < len(songs) - 1:
if songs[hi + 1] in songs_in_seq:
songs_in_seq.remove(songs[lo])
if lo == hi:
hi += 1
songs_in_seq.add(songs[hi])
lo += 1
else:
hi += 1
songs_in_seq.add(songs[hi])
longest_seq = max(longest_seq, (hi - lo) + 1)
print(longest_seq)Towers [Spec] (2024-01-27)
I went for C++ for the BST implementations:
#include <iostream>
#include <set>
#include <vector>
int main() {
int n;
std::cin >> n;
std::vector<long> cubes;
for (int i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
cubes.push_back(tmp);
}
std::multiset<long> towerTops;
for (auto cube : cubes) {
towerTops.insert(cube);
const auto &it = towerTops.upper_bound(cube);
if (it != towerTops.end()) {
towerTops.erase(it);
}
}
std::cout << towerTops.size() << std::endl;
return 0;
}Traffic Lights [Spec] (2024-01-28)
I don’t like this problem description. It’s not very clear how it’s meant to work, so I spent a long time trying ideas on the example until something worked.
I initially thought there were “units”, and a traffic light would take up one whole unit. Therefore, for the example input of and , I sketched out the example and found my interpretation to be wrong:
012345678 passage lengths: [9]
012 45678 passage lengths: [3, 5] longest passage: 5
012 45 78 passage lengths: [3, 2, 2] longest passage: 3
01 45 78 passage lengths: [2, 2, 2] longest passage: 2I then tried interpreting the positions as zero-length boundaries, which was also wrong:
012345678 passage lengths: [9]
012 345678 passage lengths: [3, 6] longest passage: 6
012 345 678 passage lengths: [3, 3, 3] longest passage: 3
01 2 345 678 passage lengths: [2, 1, 3, 3] longest passage: 3012345678 passage lengths: [9]
0123 45678 passage lengths: [4, 5] longest passage: 5
0123 456 78 passage lengths: [4, 3, 2] longest passage: 4
012 3 456 78 passage lengths: [3, 1, 3, 2] longest passage: 3Only when I considered position to implicitly come with a traffic light did the example make sense:
01234567 passage lengths: [8]
012 34567 passage lengths: [3, 5] longest passage: 5
012 345 67 passage lengths: [3, 3, 2] longest passage: 3
01 2 345 67 passage lengths: [2, 1, 3, 2] longest passage: 3I went for C++ for the BST implementations. It went awfully close to TLE’ing (it took 0.98-0.99s for many tests).
#include <iostream>
#include <set>
#include <vector>
int main() {
int x, n;
std::vector<long> p;
std::cin >> x >> n;
for (int i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
p.push_back(tmp);
}
std::multiset<long> lengths {x};
std::set<long> segments {0, x};
for (const auto &mid : p) {
auto it = segments.upper_bound(mid);
const long hi = *it;
const long lo = *(--it);
lengths.erase(lengths.find(hi - lo));
lengths.insert(mid - lo);
lengths.insert(hi - mid);
segments.insert(mid);
std::cout << *lengths.rbegin() << std::endl;
}
return 0;
}I also had the idea to iterate in reverse and use union find to merge together intervals. It turned out very cursed, but somehow runs faster than my initial C++ implementation, even in CPython3:
TODO: There should be a better solution. I should meditate on this some more.
#!/usr/bin/env python3
from itertools import pairwise, chain
(x, _) = [int(x) for x in input().strip().split()]
p = [int(x) for x in input().strip().split()]
sorted_p = sorted(p)
p_to_interval = {v: i for i, v in enumerate(sorted_p, start=1)}
intervals = list(pairwise(chain((0,), sorted(p), (x,))))
groups = list(range(len(intervals)))
def canonical(i):
if i != groups[i]:
groups[i] = canonical(groups[i])
return groups[i]
group_sizes = [b - a for a, b in intervals]
solution = [max(group_sizes)]
for pv in reversed(p):
i = p_to_interval[pv]
j = canonical(i - 1)
group_sizes[j] += group_sizes[i]
groups[i] = j
solution.append(max(solution[-1], group_sizes[j]))
print(" ".join(str(v) for v in reversed(solution[:-1])))Josephus Problem I [Spec] (2024-01-29)
I used union find to calculate skips:
#!/usr/bin/env python3
n = int(input())
skips = list(range(n))
def canonical(i):
if i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
cur = 0
for _ in range(n):
nxt = canonical((cur + 1) % n)
print(nxt + 1)
cur = skips[nxt] = canonical((nxt + 1) % n)Rewritten in C++:
#include <iostream>
#include <vector>
#include <functional>
int main() {
long n, k;
std::cin >> n >> k;
std::vector<long> skips;
for (long i = 0; i < n; ++i) skips.push_back(i);
const std::function<long(long)> canonical = [&](const long i){
if (i != skips[i]) skips[i] = canonical(skips[i]);
return skips[i];
};
long cur = 0;
for (long i = 0; i < n; ++i) {
cur = canonical((cur + 1) % n);
std::cout << cur + 1 << std::endl;
skips[cur] = canonical((cur + 1) % n);
cur = skips[cur];
}
return 0;
}Along the way, I learnt something interesting about chain assignments in Python:
In trying to refactor my solution to something nicer, I found this version to fail:
#!/usr/bin/env python3
n = int(input())
skips = list(range(n))
def canonical(i):
if i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
cur = 0
for _ in range(n):
cur = canonical((cur + 1) % n)
print(cur + 1)
cur = skips[cur] = canonical((cur + 1) % n)As it turns out, Python chained assignments work by evaluating the right-most expression, then assigning to the remaining targets from left to right (source):
Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> m = {1: 2}
>>> i = 1
>>> i = m[i] = "x"
>>> i
'x'
>>> m
{1: 2, 'x': 'x'}In the example above, if "x" assigns to m[i] first before assigning m[i] to i, you’d expect it to behave like:
Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> m = {1: 2}
>>> i = 1
>>> m[i] = "x"
>>> i = m[i]
>>> i
'x'
>>> m
{1: 'x'}But instead, it behaves like:
Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> m = {1: 2}
>>> i = 1
>>> i = "x"
>>> m[i] = "x"
>>> i
'x'
>>> m
{1: 2, 'x': 'x'}So if I wanted to refactor away the explicit new variable nxt, it would have to be rewritten as:
#!/usr/bin/env python3
n = int(input())
skips = list(range(n))
def canonical(i):
if i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
cur = 0
for _ in range(n):
cur = canonical((cur + 1) % n)
print(cur + 1)
skips[cur] = canonical((cur + 1) % n)
cur = skips[cur]This version passes all tests.
I also wrote a much simpler solution that passes according to my understanding of the problem, but it doesn’t pass the tests:
This solution assumes that the current child will remove the child before them. For example, suppose we have four children:
1 2 3 4Child 1 will remove child 4:
1 2 3
^Child 2 will remove child 1:
2 3
^Child 3 will remove child 2:
3
^And child 3 will also remove itself. Therefore the solution for four children would be 4 1 2 3.
Python implementation:
#!/usr/bin/env python3
n = int(input())
print(n, " ".join(str(x) for x in range(1, n)))TODO: I’m actually not yet sure why that solution isn’t considered valid. Nothing in the problem specification seems to disallow it.
Alternative C++ solution using BST/std::set, though it somehow runs slower than the Python solution even with IO desync:
#include <iostream>
#include <set>
int main() {
long n, k;
std::cin >> n >> k;
std::set<long> nums;
for (long i = 0; i < n; ++i) nums.insert(i);
auto it = nums.begin();
while (nums.size()) {
++it;
if (it == nums.end()) it = nums.begin();
long v0 = *it;
std::cout << v0 + 1 << std::endl;
++it;
if (it == nums.end()) it = nums.begin();
long v1 = *it;
nums.erase(v0);
it = nums.find(v1);
}
return 0;
}Another solution, this time using list shifting for fast deletions. Actually runs faster than my previous solutions (including C++). The item deletion overhead is fast since we’re deleting half of the set at any given time. Implementation:
#!/usr/bin/env python3
n = int(input())
cur = list(range(1, n + 1))
do_print = False
while len(cur):
lo = 0
for hi in range(len(cur)):
if do_print:
print(cur[hi])
else:
cur[lo] = cur[hi]
lo += 1
do_print = (do_print == False)
del cur[lo:]I rewrote it in C++, but it’s somehow slower than the Python version:
#include <iostream>
#include <vector>
#include <functional>
int main() {
long n;
std::cin >> n;
bool doPrint = false;
std::vector<long> cur;
for (long i = 1; i <= n; ++i) cur.push_back(i);
while (!cur.empty()) {
auto lo = 0;
for (long hi = 0; ((unsigned long) hi) < cur.size(); ++hi) {
if (doPrint) {
std::cout << cur[hi] << std::endl;
} else {
cur[lo] = cur[hi];
++lo;
}
doPrint = (doPrint == false);
}
cur.resize(lo);
}
return 0;
}Josephus Problem II [UNFINISHED] [Spec] (2024-01-29)
I used my Josephus Problem I union find solution as a starting point. After a cold start of misunderstanding the problem specification, my first logically correct solution ran out of time and caused a stack overflow with the default recursion limit). Not unexpected since it’s for quite large and :
#!/usr/bin/env python3
(n, k) = [int(s) for s in input().strip().split()]
skips = list(range(n))
def canonical(i):
if i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
cur = 0
for _ in range(n):
for _ in range(k):
cur = canonical((cur + 1) % n)
print(cur + 1)
skips[cur] = canonical((cur + 1) % n)
cur = canonical((cur + 1) % n)I tried adding a modulo to cut down on the -iterations. It passes some more tests, but as expected, it still TLE’s and causes a stack overflow:
#!/usr/bin/env python3
(n, k) = [int(s) for s in input().strip().split()]
skips = list(range(n))
def canonical(i):
if i != skips[i]:
skips[i] = canonical(skips[i])
return skips[i]
cur = 0
for i in range(n):
for _ in range(k % (n - i)):
cur = canonical((cur + 1) % n)
print(cur + 1)
skips[cur] = canonical((cur + 1) % n)
cur = canonical((cur + 1) % n)The only difference from the first TLE’d solution is these lines:
for i in range(n):
for _ in range(k % (n - i)):TODO: Finish this
Nested Ranges Check [Spec] (2024-01-31)
My first attempt TLE’d, but otherwise seems promising in terms of correctness:
#!/usr/bin/env python3
from sys import stdin
from collections import Counter, defaultdict
stdin.readline()
ranges = [
(*(int(x) for x in s.strip().split()), i) # (start, end, index)
for i, s in enumerate(stdin.readlines())
]
grouped = defaultdict(list)
cnt = Counter() # {(start, end): count}
for tup in ranges:
grouped[tup[0]].append(tup)
cnt[(tup[0], tup[1])] += 1
for v in grouped.values():
v.sort(key=lambda x: x[1])
grouped = sorted(grouped.items())
# check if range contains another range
solution = [0]*len(ranges)
cum_min_end = grouped[-1][1][-1][1] + 1 # arbitrary large end
for start, lst in reversed(grouped):
for _, end, i in lst:
if (cnt[(start, end)] > 1) or (end >= cum_min_end):
solution[i] = 1
cum_min_end = min(cum_min_end, end) # only updates at the start of a group... hmmmm....
print(" ".join(str(x) for x in solution))
# check if range is contained in another range
solution = [0]*len(ranges)
cum_max_end = 0
for start, lst in grouped:
for _, end, i in reversed(lst):
if (cnt[(start, end)] > 1) or (end <= cum_max_end):
solution[i] = 1
cum_max_end = max(cum_max_end, end) # only updates at the start of a group... hmmmm....
print(" ".join(str(x) for x in solution))Rewriting it for C++ passed all tests! Full solution:
#include <algorithm>
#include <iostream>
#include <vector>
#include <limits>
#include <ranges>
typedef std::tuple<long, long, long> Tup3;
int main() {
int n;
std::cin >> n;
std::unordered_map<long, std::vector<Tup3>> groupedMap; // grouped[start] = ranges subset
std::unordered_map<long, std::unordered_map<long, long>> cnt; // cnt[start][end] = count
for (int i = 0; i < n; ++i) {
long start, end;
std::cin >> start >> end;
groupedMap[start].emplace_back(start, end, i);
++cnt[start][end];
}
// convert groupedMap to a vector, and sort both inner and outer
std::vector<std::pair<long, std::vector<Tup3>>> grouped;
for (auto &[start, lst] : groupedMap) {
std::sort(lst.begin(), lst.end(),
[](auto a, auto b){return std::get<1>(a) < std::get<1>(b);}
);
grouped.emplace_back(start, std::move(lst));
}
std::sort(grouped.begin(), grouped.end());
// check if range contains another range
std::vector<char> solution(n, '0');
long cumMinEnd = std::numeric_limits<long>::max();
for (auto &[start, lst] : std::ranges::reverse_view(grouped)) {
for (auto &[_, end, i] : lst) {
if ((cnt.at(start).at(end) > 1) || (end >= cumMinEnd)) {
solution[i] = '1';
}
cumMinEnd = std::min(cumMinEnd, end);
}
}
for (auto &c : solution) std::cout << c << " ";
std::cout << std::endl;
// check if range is contained in another range
std::fill(solution.begin(), solution.end(), '0');
long cumMaxEnd = 0;
for (auto &[start, lst] : grouped) {
for (auto &[_, end, i] : std::ranges::reverse_view(lst)) {
if ((cnt.at(start).at(end) > 1) || (end <= cumMaxEnd)) {
solution[i] = '1';
}
cumMaxEnd = std::max(cumMaxEnd, end);
}
}
for (auto &c : solution) std::cout << c << " ";
std::cout << std::endl;
return 0;
}I also made some further modifications to add I/O desync and switch solution to std::vector<bool>. Both very slightly improved performance.
TODO: Maybe we can still get more significant performance wins?
Nested Ranges Count [UNFINISHED] [Spec] (2024-02-01)
I started by looking into how to count intervals contained within another interval.
My first idea was to sort the ranges twice (once sorted by start point and once sorted by endpoint), and calculate cumulative counts, to be stored in BSTs/std::map. In an attempt to make this idea work, I looked into possible ways to write out the set arithmetic, but I conclude that it’s unlikely to be a useful approach on its own.
Let’s have a look at a concrete example:
t====
a-
b--
c--- d---
e--- f---
g------------Above, we have one target interval labelled t, and seven other intervals that are also part of the set.
I see a few different operations to quickly count/enumerate relevant subsets just by a simple inequality. Here’s a minimal subset of operations:
- Total other intervals:
- Intervals with starting points after the start of
t: - Intervals with starting points after the end of
t: - Intervals with ending points after the start of
t: - Intervals with ending points after the end of
t:
For completeness, let’s derive the opposites:
- Intervals with starting points before the start of
t: - Intervals with starting points before the end of
t: - Intervals with ending points before the start of
t: - Intervals with ending points before the end of
t:
Unsurprisingly, the numbers of the opposites are the same since our example is quite symmetrical.
The theoretically useful thing here is that it’s relatively quick () to query the count of these subsets after constructing a BST in . So maybe we can construct an equation that simply operates on the sizes of these subsets?
However, I feel like it’s unlikely to be a useful solution since you need to be able to query for both the start and end points simultaneously.
Let’s play around with the example a bit.
A good place to start might be #2 (intervals with starting points after the start of t):
t====
a-
b--
d---
f---But how do we filter out interval d and f?
Let’s try just querying for #5 (intervals with ending points after the start of t):
t====
d---
f---
g------------But how do we filter out interval g from query #5?
I haven’t figured a solution to this problem yet. I imagine it might be possible to prove that this approach is possible or impossible, but I’m not going into that right now.
An evolution of the idea might be to incrementally build the cumulative counts data structure as you iterate through the list of ranges, sorted by starting point.
For example, maybe you start with the intervals at the lowest starting point, which we’ll pretend to be . You’d have a cumulative counts data structure for every possible interval since all intervals will start with at least the lowest starting point. You’d go through all the intervals with starting point , querying for the number of intervals with endpoints no further than the currently-visited interval.
After you’re done with all intervals with starting point , you go to the next-highest starting point, which let’s pretend it’s . This requires us to modify the cumulative counts data structure to discard all intervals with starting points before .
This process is simply repeated until we exhaust all intervals.
Alternatively (and probably better), you could do the reverse by starting with the highest starting point and working your way backwards to the lowest starting point.
However, the trouble is finding a data structure that lets you insert fast while also letting you quickly query cumulative counts. A BST in lets you insert in but is probably difficult to get a cumulative count without sequential counting. A array that we keep sorted lets you get a cumulative count in potentially due to binary search and count (ignoring multiplicity edge cases for now), but suffers from insertions.
Therefore, this is probably not the right approach.
TODO: Continue!
Room Allocation [Spec] (2024-02-02)
I attempted a straightforward Python implementation using heapq but it TLE’s on one test case (a test case that seems quite significantly harder than even my longest-running accepted test case). The solution otherwise seems logically correct, and passes all the other test cases within the time limit:
#!/usr/bin/env python3
from sys import stdin
from heapq import heappush, heappop
stdin.readline()
bookings = sorted(
(*(int(x) for x in s.strip().split()), i) # (start, end, i)
for i, s in enumerate(stdin.readlines())
)
solution = [None]*len(bookings)
rooms_pq = [(bookings[0][0], 1)] # [(earliest acceptable start, room number), ...]
for start, end, i in bookings:
if rooms_pq[0][0] <= start:
(_, room_number) = heappop(rooms_pq)
else:
room_number = len(rooms_pq) + 1
solution[i] = str(room_number)
heappush(rooms_pq, (end + 1, room_number))
print(len(rooms_pq))
print(" ".join(solution))Rewriting it in C++ passed all tests:
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
typedef std::pair<long, long> Room;
typedef std::priority_queue<Room, std::vector<Room>, std::greater<Room>> RoomsPQ;
int main() {
long n;
std::cin >> n;
std::vector<std::tuple<long, long, long>> bookings;
for (long i = 0; i < n; ++i) {
long start, end;
std::cin >> start >> end;
bookings.emplace_back(start, end, i);
}
std::sort(bookings.begin(), bookings.end());
std::vector<long> solution(n);
// [(earliest acceptable start, room number), ...]
RoomsPQ rooms;
rooms.push(std::make_pair(std::get<0>(bookings[0]), 1));
for (const auto &[start, end, i] : bookings) {
const auto &top = rooms.top();
long roomNum = top.second;
if (top.first <= start) {
rooms.pop();
} else {
roomNum = rooms.size() + 1;
}
solution[i] = roomNum;
rooms.push(std::make_pair(end + 1, roomNum));
}
std::cout << rooms.size() << std::endl;
for (const long &v : solution) std::cout << v << " ";
std::cout << std::endl;
return 0;
}In an attempt to get a Python solution working, I tried batching start times (it makes sense in context) but it generally caused a slight slowdown compared to my first Python attempt:
#!/usr/bin/env python3
from sys import stdin
from heapq import heappush, heappop
stdin.readline()
bookings = sorted(
(*(int(x) for x in s.strip().split()), i) # (start, end, i)
for i, s in enumerate(stdin.readlines())
)
solution = [None]*len(bookings)
rooms_pq = [bookings[0][0]] # [earliest acceptable start, ...]
rooms_batches = {bookings[0][0]: [1]} # {earliest acceptable start: indices, ...}
last_room = 1
for start, end, i in bookings:
earliest_start = rooms_pq[0]
if earliest_start <= start:
room_number = rooms_batches[earliest_start].pop()
if len(rooms_batches[earliest_start]) == 0:
del rooms_batches[earliest_start]
heappop(rooms_pq)
else:
last_room += 1
room_number = last_room
solution[i] = str(room_number)
new_earliest_start = end + 1
if new_earliest_start in rooms_batches:
rooms_batches[new_earliest_start].append(room_number)
else:
heappush(rooms_pq, new_earliest_start)
rooms_batches[new_earliest_start] = [room_number]
print(last_room)
print(" ".join(solution))I also tried taking it further by replacing the priority queue with a sorted queue, but it was even slower:
#!/usr/bin/env python3
from sys import stdin
from heapq import heappush, heappop
stdin.readline()
bookings = sorted(
(*(int(x) for x in s.strip().split()), i) # (start, end, i)
for i, s in enumerate(stdin.readlines())
)
# earliest acceptable starts
rooms_q_head = 0
rooms_q = [end + 1 for _, end, _ in bookings]
rooms_q.append(bookings[0][0])
rooms_q.sort()
# prune duplicates
lo = 0
for hi in range(1, len(rooms_q)):
if rooms_q[lo] != rooms_q[hi]:
lo += 1
rooms_q[lo] = rooms_q[hi]
del rooms_q[lo+1:]
# {earliest acceptable start: indices, ...}
rooms_batches = {earliest_start: [] for earliest_start in rooms_q}
rooms_batches[bookings[0][0]].append(1)
last_room = 1
solution = [None]*len(bookings)
for start, end, i in bookings:
earliest_start = rooms_q[rooms_q_head]
if earliest_start <= start:
room_number = rooms_batches[earliest_start].pop()
if len(rooms_batches[earliest_start]) == 0:
rooms_q_head += 1
else:
last_room += 1
room_number = last_room
solution[i] = str(room_number)
new_earliest_start = end + 1
rooms_batches[end + 1].append(room_number)
print(last_room)
print(" ".join(solution))Factory Machines [Spec] (2024-02-05)
The first thing I tried was a relatively naive solution, but I didn’t properly read the problem bounds at the time, which says . With these bounds, it’s clear why it doesn’t pass. I wrote it in Python and then rewrote in C++:
#!/usr/bin/env python3
from heapq import heapify, heappush, heappop
(_, prod_target) = [int(s) for s in input().strip().split()]
machines = sorted(int(s) for s in input().strip().split())
next_free = [(dur, dur) for dur in machines] # [(new total duration, machine duration), ...]
heapify(next_free)
total_dur = 0
for _ in range(prod_target):
(new_total_dur, machine_dur) = heappop(next_free)
total_dur = max(total_dur, new_total_dur)
heappush(next_free, (new_total_dur + machine_dur, machine_dur))
print(total_dur)#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
typedef std::pair<long, long> Tup2;
typedef std::vector<Tup2> NextFreeContainer;
typedef std::priority_queue<Tup2, NextFreeContainer, std::greater<Tup2>> NextFree;
int main() {
int n, prodTarget;
std::cin >> n >> prodTarget;
NextFreeContainer nextFreeContainer;
for (int i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
nextFreeContainer.emplace_back(tmp, tmp);
}
NextFree nextFree(std::greater<Tup2>(), std::move(nextFreeContainer));
long totalDur = 0;
for (long i = 0; i < prodTarget; ++i) {
const auto [newTotalDur, machineDur] = nextFree.top();
nextFree.pop();
if (newTotalDur > totalDur) totalDur = newTotalDur;
nextFree.emplace(newTotalDur + machineDur, machineDur);
}
std::cout << totalDur << std::endl;
return 0;
}The next thing I did was a very low-effort adaptation to start with a binary search to go almost the whole way, and then getting the final solution by applying my original naive solution, which wouldn’t have a lot left to do after binary search has already done the work. It’s almost certainly possible to just make it a pure binary search, but doing it this way allows me to be lazy and be loose with the algorithm design to at least get something to pass, and I already had the naive code anyway. Unfortunately, it had an extremely trivial bug, causing my initial implementations to TLE:
#!/usr/bin/env python3
from heapq import heapify, heappush, heappop
(_, prod_target) = [int(s) for s in input().strip().split()]
machines = sorted(int(s) for s in input().strip().split())
#
# Binary search for an estimate
#
prod_remaining = prod_target # modify later
est_total_dur = 0
bitmask = 1 << 31
while bitmask:
new_est_total_dur = est_total_dur | bitmask
new_prod_remaining = prod_target
for machine_dur in machines:
prod = new_est_total_dur // machine_dur
new_prod_remaining -= prod
if new_prod_remaining <= 0:
break
if new_prod_remaining > 0:
est_total_dur = new_est_total_dur
prod_remaining = new_prod_remaining
bitmask >>= 1
total_durs = [est_total_dur - (est_total_dur % machine_dur) for machine_dur in machines]
#
# Heap-based algo to get the rest
#
# [(new total duration, machine duration), ...]
next_free = [(tot_dur + m_dur, m_dur) for m_dur, tot_dur in zip(machines, total_durs)]
heapify(next_free)
overall_dur = 0 # works since we assume there's always remaining product
for _ in range(prod_remaining):
(new_total_dur, machine_dur) = heappop(next_free)
overall_dur = max(overall_dur, new_total_dur)
heappush(next_free, (new_total_dur + machine_dur, machine_dur))
print(overall_dur)#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
typedef std::pair<long, long> Tup2;
typedef std::vector<Tup2> NextFreeContainer;
typedef std::priority_queue<Tup2, NextFreeContainer, std::greater<Tup2>> NextFree;
int main() {
long n, prodTarget;
std::cin >> n >> prodTarget;
std::vector<long> machines;
for (long i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
machines.push_back(tmp);
}
long long prodRemaining = prodTarget;
long long estTotalDur = 0;
long long bitmask = 1;
bitmask <<= 31; // how come just doing (1 << 31) doesn't work?
while (bitmask) {
long long newProdRemaining = prodTarget;
long long newEstTotalDur = estTotalDur | bitmask;
for (const auto &machineDur : machines) {
newProdRemaining -= newEstTotalDur / machineDur;
if (newProdRemaining <= 0) break;
}
if (newProdRemaining > 0) {
estTotalDur = newEstTotalDur;
prodRemaining = newProdRemaining;
}
bitmask >>= 1;
if (bitmask < 0) return 0;
}
NextFreeContainer nextFreeContainer;
for (const auto &machineDur : machines) {
const long long totalDur = estTotalDur - (estTotalDur % machineDur);
nextFreeContainer.emplace_back(totalDur + machineDur, machineDur);
}
NextFree nextFree(std::greater<Tup2>(), std::move(nextFreeContainer));
long long totalDur = 0;
for (long i = 0; i < prodRemaining; ++i) {
const auto [newTotalDur, machineDur] = nextFree.top();
nextFree.pop();
if (newTotalDur > totalDur) totalDur = newTotalDur;
nextFree.emplace(newTotalDur + machineDur, machineDur);
}
std::cout << totalDur << std::endl;
return 0;
}The issue was that my binary search only covered outputs of up to . However, outputs could actually be even larger, meaning that if an output was actually something like , the second stage of the algorithm (the naive stage) may still have a lot more products left to process.
This actually eluded me for several days until I actually read the test cases I TLE’d on and realized how big the outputs were. The only change I had to make was to change from bitmask = 1 << 31 to bitmask = 1 << 63, leading to my first solution (written in Python and C++) that passes all tests:
#!/usr/bin/env python3
from heapq import heapify, heappush, heappop
(_, prod_target) = [int(s) for s in input().strip().split()]
machines = sorted(int(s) for s in input().strip().split())
#
# Binary search for an estimate
#
prod_remaining = prod_target # modify later
est_total_dur = 0
bitmask = 1 << 63
while bitmask:
new_est_total_dur = est_total_dur | bitmask
new_prod_remaining = prod_target
for machine_dur in machines:
prod = new_est_total_dur // machine_dur
new_prod_remaining -= prod
if new_prod_remaining <= 0:
break
if new_prod_remaining > 0:
est_total_dur = new_est_total_dur
prod_remaining = new_prod_remaining
bitmask >>= 1
#
# Heap-based algo to get the rest
#
# [(new total duration, machine duration), ...]
next_free = [(est_total_dur - (est_total_dur % m_dur) + m_dur, m_dur) for m_dur in machines]
heapify(next_free)
overall_dur = 0 # works since we assume there's always remaining product
for _ in range(prod_remaining):
(new_total_dur, machine_dur) = heappop(next_free)
overall_dur = max(overall_dur, new_total_dur)
heappush(next_free, (new_total_dur + machine_dur, machine_dur))
print(overall_dur)#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
typedef std::pair<long, long> Tup2;
typedef std::vector<Tup2> NextFreeContainer;
typedef std::priority_queue<Tup2, NextFreeContainer, std::greater<Tup2>> NextFree;
int main() {
long n, prodTarget;
std::cin >> n >> prodTarget;
std::vector<long> machines;
for (long i = 0; i < n; ++i) {
long tmp;
std::cin >> tmp;
machines.push_back(tmp);
}
long long prodRemaining = prodTarget;
long long estTotalDur = 0;
long long bitmask = 1;
bitmask <<= 62; // how come just doing (1 << 31) doesn't work?
while (bitmask) {
long long newProdRemaining = prodTarget;
long long newEstTotalDur = estTotalDur | bitmask;
for (const auto &machineDur : machines) {
newProdRemaining -= newEstTotalDur / machineDur;
if (newProdRemaining <= 0) break;
}
if (newProdRemaining > 0) {
estTotalDur = newEstTotalDur;
prodRemaining = newProdRemaining;
}
bitmask >>= 1;
if (bitmask < 0) return 0;
}
NextFreeContainer nextFreeContainer;
for (const auto &machineDur : machines) {
const long long totalDur = estTotalDur - (estTotalDur % machineDur);
nextFreeContainer.emplace_back(totalDur + machineDur, machineDur);
}
NextFree nextFree(std::greater<Tup2>(), std::move(nextFreeContainer));
long long totalDur = 0;
for (long i = 0; i < prodRemaining; ++i) {
const auto [newTotalDur, machineDur] = nextFree.top();
nextFree.pop();
if (newTotalDur > totalDur) totalDur = newTotalDur;
nextFree.emplace(newTotalDur + machineDur, machineDur);
}
std::cout << totalDur << std::endl;
return 0;
}TODO: I think a purely binary search solution should be possible, without the naive heap-based part. I should try it! I’m just feeling a bit lazy rn
TODO: Is there a nicer solution than binary search? Or maybe a faster way to calculate how many products can be made at a given point in time? It feels like there should be something better.
Tasks and Deadlines [Spec] (2024-02-05)
I think the key to this question is realizing that even if you finish a task super-early at the expense of doing another task later and possibly even eating a negative reward, the super-early task could cancel it out. Therefore, the most optimal play is to just worry about how fast you can do tasks, and always do the shortest task before a longer task, that way you collect the reward as soon as possible.
#!/usr/bin/env python3
from sys import stdin
stdin.readline()
tasks = sorted(tuple(int(x) for x in s.strip().split()) for s in stdin.readlines())
(t, total_reward) = (0, 0)
for duration, deadline in tasks:
t += duration
total_reward += deadline - t
print(total_reward)Reading Books [UNFINISHED] [Spec] (2024-02-06)
TODO: I have some ideas, but otherwise haven’t come up with a possible solution for this problem yet.
Sum of Three Values [Spec] (2024-02-12)
For a question this simple, this one took an embarrassing amount of time for me to get!
My initial solution was to incrementally build a sum of two values dictionary, then for each value, we check if there is a sum of two other values that we can add to it to sum to the target . However, the solution is quite slow:
#!/usr/bin/env python3
def run():
(_, target) = [int(x) for x in input().strip().split()]
nums = [int(x) for x in input().strip().split()]
pairs = {}
for i1, v1 in enumerate(nums):
if v1 in pairs:
print(i1 + 1, pairs[v1][0] + 1, pairs[v1][1] + 1)
return
for i2, v2 in enumerate(nums[:i1]):
v3 = target - v1 - v2
if v3 > 0:
pairs[v3] = (i1, i2)
print("IMPOSSIBLE")
run()I took an embarrassing amount of time writing increasingly optimized versions of it, and even contemplated redoing it in C++.
However, my breakthrough came after realizing we can run a two-pointer algorithm as the inner loop, which is much lighter-weight than dictionary-building even though they’re both :
#!/usr/bin/env python3
def run():
(_, target) = [int(x) for x in input().strip().split()]
nums = [(int(x), i) for i, x in enumerate(input().strip().split()) if (int(x) - 1 < target)]
nums.sort()
lowest_i = 0
while (len(nums) >= 3) and (nums[0][0] + nums[1][0] + nums[-1][0] > target):
nums.pop()
for i, (v, _) in enumerate(nums[:-2]):
if target - nums[-1][0] - nums[-2][0] - v <= 0:
break
lowest_i = i
for i, (v, pos1) in enumerate(nums[lowest_i:], start=lowest_i):
(lo, hi) = (lowest_i, len(nums) - 1)
while lo < hi:
x = v + nums[lo][0] + nums[hi][0]
if (x > target) or (hi == i):
hi -= 1
elif (x < target) or (lo == i):
lo += 1
else:
print(pos1 + 1, nums[lo][1] + 1, nums[hi][1] + 1)
return
print("IMPOSSIBLE")
run()Sum of Four Values [Spec] (2024-02-13)
Having done Sum of Three Values, adapting a similar two-pointer approach was straightforward. My solution builds a sum-of-two-values list and then carries out the two-pointer approach on it:
#!/usr/bin/env python3
from itertools import combinations, product
from collections import defaultdict
def run():
(_, target) = [int(x) for x in input().strip().split()]
nums = [(int(x), i) for i, x in enumerate(input().strip().split()) if (int(x) - 1 < target)]
nums.sort()
lowest_i = 0
while (len(nums) >= 4) and (nums[0][0] + nums[1][0] + nums[2][0] + nums[-1][0] > target):
nums.pop()
for i, (v, _) in enumerate(nums[:-3]):
if target - nums[-1][0] - nums[-2][0] - nums[-3][0] - v <= 0:
break
lowest_i = i
pairs = defaultdict(list)
for (v1, i1), (v2, i2) in combinations(nums[lowest_i:], 2):
pairs[v1 + v2].append((i1, i2))
pairs = list(pairs.items())
pairs.sort(key=lambda x: x[0])
(lo, hi) = (0, len(pairs) - 1)
while lo <= hi:
x = pairs[lo][0] + pairs[hi][0]
if x > target:
hi -= 1
elif x < target:
lo += 1
else:
check = set()
for (i1, i2), (i3, i4) in product(pairs[lo][1], pairs[hi][1]):
check.clear()
check.update((i1, i2, i3, i4))
if len(check) == 4:
print(*(i + 1 for i in check))
return
hi -= 1 # arbitrary
print("IMPOSSIBLE")
run()Nearest Smaller Values [Spec] (2024-02-13)
Right off the bat, a monotonic stack seems to fit the problem very well. It’s a very straightforward algorithm, though my first attempt unfortunately involves a binary search since I was still working through how you’d query the stack:
#!/usr/bin/env python3
from bisect import bisect_left
input()
nums = [int(s) for s in input().strip().split()]
stack = [(2e9, -1)]
for i, v in enumerate(nums):
j = bisect_left(stack, v, key=lambda x: x[0]) - 1
print(0 if (j < 0) else stack[j][1] + 1)
while len(stack) and (stack[-1][0] >= v):
stack.pop()
stack.append((v, i))After submitting that initial solution, I quickly fixed it up to remove the unnecessary binary search:
#!/usr/bin/env python3
input()
nums = [int(s) for s in input().strip().split()]
stack = [(2e9, -1)]
for i, v in enumerate(nums):
while len(stack) and (stack[-1][0] >= v):
stack.pop()
print((stack[-1][1] + 1) if len(stack) else 0)
stack.append((v, i))Subarray Sums I [Spec] (2024-02-13)
#!/usr/bin/env python3
(_, target) = [int(s) for s in input().strip().split()]
nums = [int(s) for s in input().strip().split()]
(acc, leftsums, solution) = (0, {0}, 0)
for v in nums:
acc += v
if acc - target in leftsums:
solution += 1
leftsums.add(acc)
print(solution)Subarray Sums II [Spec] (2024-02-14)
My first attempt was to adapt my Subarray Sums I solution, but to use a multiset (the Counter type from the Python standard library) instead of a regular set. However, it kept TLE’ing on 1-2 tests depending on whether you choose CPython3 or PyPy3. I feel like maybe some people devised some very clever Python dict hashing worst-case input sequences! Full implementation:
#!/usr/bin/env python3
from collections import Counter
(_, target) = [int(s) for s in input().strip().split()]
nums = [int(s) for s in input().strip().split()]
(acc, leftsums, solution) = (0, Counter((0,)), 0)
for v in nums:
acc += v
if acc - target in leftsums:
solution += leftsums[acc - target]
leftsums[acc] += 1
print(solution)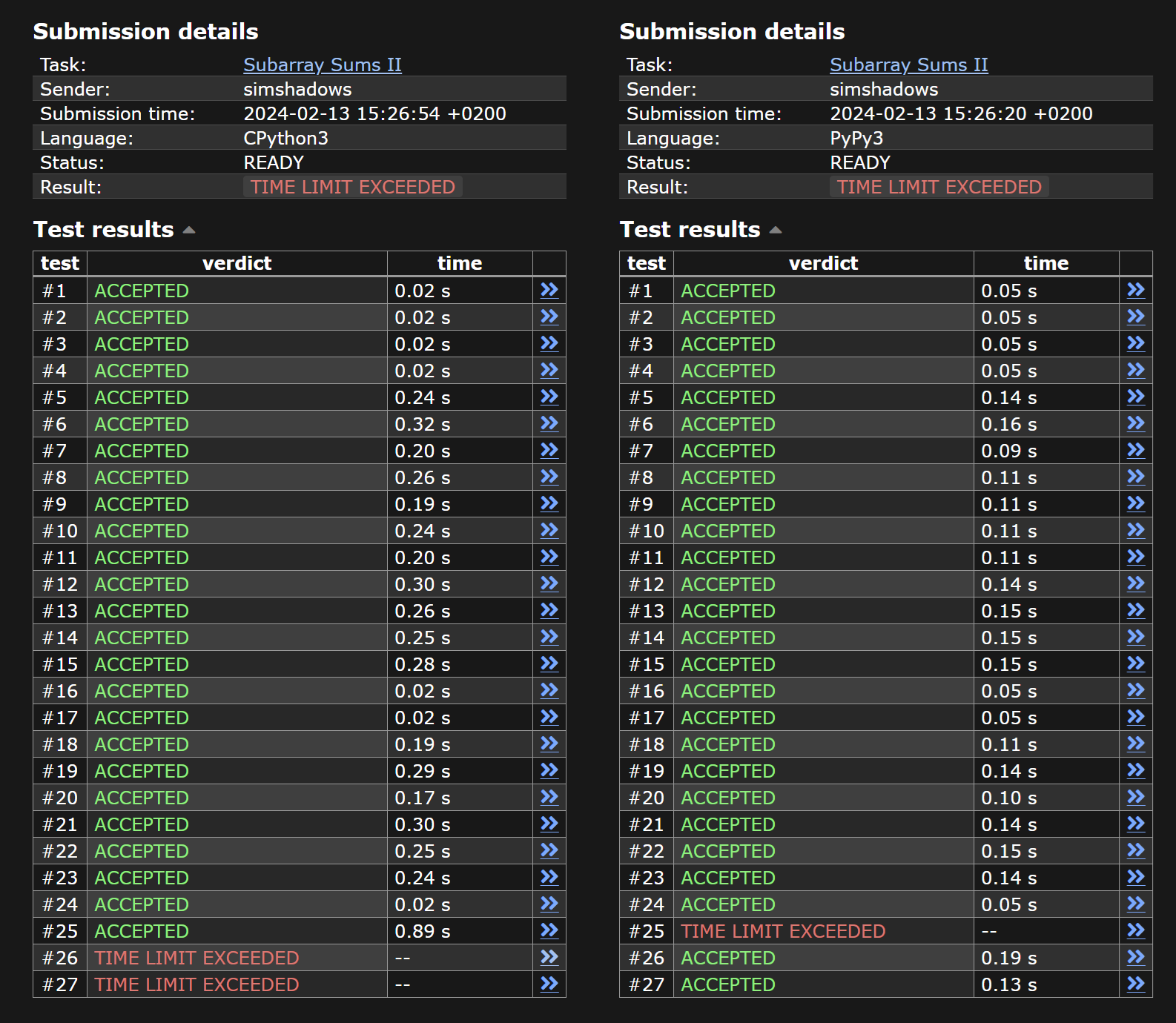
It feels like there isn’t much more you can do with Python to make this initial attempt work. However, I came up with a new idea that avoids hashing. The approach uses a sliding window strategy that first builds a sorted list of tuples of cumulative sums with indices (named accs). Importantly, this array is sorted first by the cumulative sum, and then by the index. Without sorting also by index, this algorithm won’t work.
TODO: I know that the explanation below (of my first successful solution) is very difficult to understand. I want to rewrite it whenever I have the time.
We begin with two pointers (lo and hi) around the start of the list. If the two pointers don’t indicate a possible subarray sum that can add up to the target, the pointers increment appropriately until it does add up to target. For example, if the current subarray sum is bigger than target, we’d need to increment lo. If the current subarray sum is smaller than target, we’d need to increment hi.
When we do encounter a subarray sum that adds up to target, we now have to deal with the indices that make up the second part of the tuples in accs. A subarray sum is only actually valid if hi’s index is greater than lo’s index.
When we first find a potentially valid subarray sum (i.e. it adds up to target but not yet known if hi’s index is greater than lo’s index), the pointers will be at the beginning of the groups of cumulative sums. For example:
target = 3
nums = [ 7, -3, 3, -3, 1, 3, -4, 3]
accumulate(sums, initial=0) = [0, 7, 4, 7, 4, 5, 8, 4, 7]
the `i` part of `enumerate` = [0, 1, 2, 3, 4, 5, 6, 7, 8]
accs = [..., (4,2), (4,4), (4,7), ..., (7,1), (7,3), (7,8), ...]
^^^^^ ^^^^^
lo hiIn this example, we see that the subarray sum is not valid because although so it satisfies the target sum, the indices are wrong. To get the sum of the subarray nums[1:2], we need the cumulative sum at nums[1] minus the cumulative sum at nums[0]. However, since hi’s index is 1 and lo’s index is 2, this implies that the subarray sum was calculated using the cumulative sum at nums[0] minus the cumulative sum at nums[1].
TODO: The explanation above is very difficult to understand without clearer diagrams. I should make diagrams.
However, now notice what happens when we increment hi:
accs = [..., (4,2), (4,4), (4,7), ..., (7,1), (7,3), (7,8), ...]
^^^^^ ^^^^^
lo hiWe now have a valid subarray sum because lo and hi correctly implies the sum of the subarray nums[2:3].
TODO: This is extra-confusing because accs has an extra element at the beginning. I need to make this clearer somehow.
Let’s skip a few steps and consider the following state of the algorithm:
accs = [..., (4,2), (4,4), (4,7), ..., (7,1), (7,3), (7,8), ...]
^^^^^ ^^^^^
lo hilo and hi not only correctly implies the sum of the subarray nums[7:8] to equal target, but also two more subarrays nums[4:8] and nums[2:8] also equal target. We know this because there are two other cumulative sums to the left of lo with the same cumulative sum that also have indices lower than hi! It’s very easy to keep track of this sort of thing in my implementation thanks to the variables lo_acc and lo_count.
That should now be sufficient background to understand how my first successful solution works:
#!/usr/bin/env python3
from itertools import accumulate
(_, target) = [int(s) for s in input().strip().split()]
nums = [int(s) for s in input().strip().split()]
accs = sorted((v, i) for (i, v) in enumerate(accumulate(nums, initial=0)))
(lo, hi) = (0, 1)
(lo_acc, lo_count) = (accs[0][0], 1)
def inc_lo():
global lo, lo_acc, lo_count
lo += 1
# TODO: do we need to reprocess lo_acc and lo_count always lol
if lo_acc == accs[lo][0]:
lo_count += 1
else:
lo_acc = accs[lo][0]
lo_count = 1
solution = 0
while hi < len(accs):
v = accs[hi][0] - accs[lo][0]
if (v < target) or (lo == hi):
hi += 1
elif v > target:
inc_lo()
elif (accs[lo + 1][0] == lo_acc) and (accs[lo + 1][1] < accs[hi][1]):
inc_lo()
else:
if accs[lo][1] < accs[hi][1]:
solution += lo_count
hi += 1
print(solution)For completeness, I decided to see if my initial Python solution can work in C++, and it turns out that it does! Implementation:
#include <iostream>
#include <vector>
#include <unordered_map>
int main() {
long n, target;
std::cin >> n >> target;
std::vector<long> nums;
for (long i = 0; i < n; ++i) {
long v;
std::cin >> v;
nums.push_back(v);
}
std::unordered_map<long, long> leftsums;
leftsums.emplace(0, 1);
long acc = 0;
long solution = 0;
for (const auto &v : nums) {
acc += v;
const long x = acc - target;
if (leftsums.contains(x)) solution += leftsums.at(x);
++leftsums[acc];
}
std::cout << solution << std::endl;
return 0;
}Subarray Divisibility [Spec] (2024-02-14)
Clearly a followup from Subarray Sums II. This problem was initially very intimidating until I realized you can just use the modulo of the cumulative sum!
I started out with my initial attempt at Subarray Sums II (which was in Python) and modified it with the modulo trick. Unfortunately, it TLE’d in a somewhat similar way to my initial attempt at Subarray Sums II. Like Subarray Sums II, maybe the TLE’d test case was also a Python dict hashing worst-case input sequence? Implementation:
#!/usr/bin/env python3
from collections import Counter
input()
nums = [int(s) for s in input().strip().split()]
target = len(nums)
(acc, leftsums, solution) = (0, Counter((0,)), 0)
for v in nums:
acc = (acc + v) % target
if acc in leftsums:
solution += leftsums[acc]
leftsums[acc] += 1
print(solution)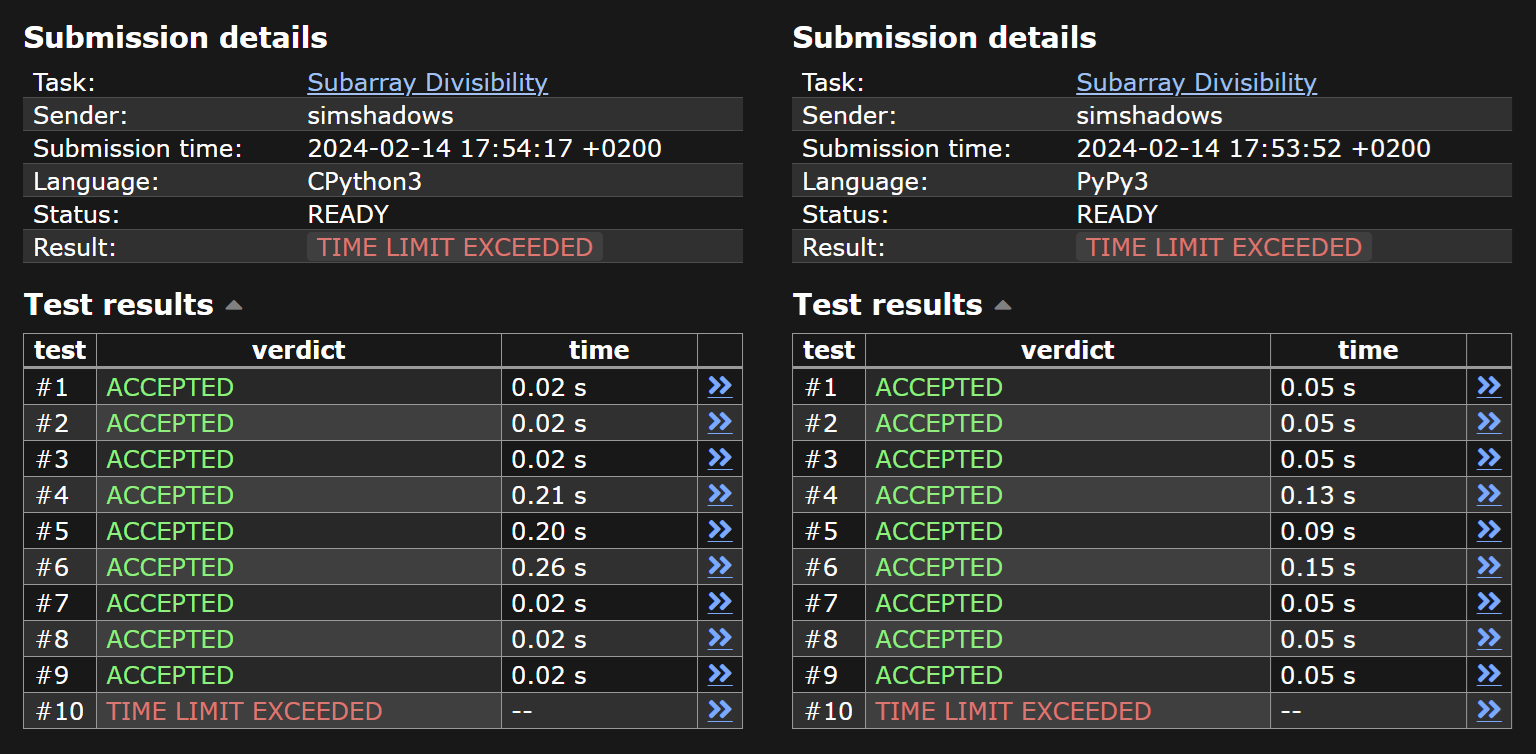
This time, I just went straight to rewriting it in C++ since I already had a C++ solution for Subarray Sums II. This became my first passing solution:
#include <iostream>
#include <vector>
#include <unordered_map>
int main() {
long n;
std::cin >> n;
std::vector<long> nums;
for (long i = 0; i < n; ++i) {
long v;
std::cin >> v;
nums.push_back(v);
}
std::unordered_map<long, long> leftsums;
leftsums.emplace(0, 1);
long acc = 0;
long solution = 0;
for (const auto &v : nums) {
acc = (((acc + v) % n) + n) % n;
if (leftsums.contains(acc)) solution += leftsums.at(acc);
++leftsums[acc];
}
std::cout << solution << std::endl;
return 0;
}I also learnt something interesting about modulo with negative numbers in C++, hence the funny (((acc + v) % n) + n) % n.
C++ is designed such that the the modulo operator % is actually always the remainder of a division. In other words, this will always be true (for ):
(a/b)*b + a%b == aTo always get a positive number, you can simply add the modulo then modding again:
positive_modulo = ((a % b) + b) % bInterestingly, the behaviour is different with Python, hence why my Python solution doesn’t need this trick.
I also went ahead and adapted my Python sliding window solution for Subarray Sums II:
#!/usr/bin/env python3
from itertools import accumulate
input()
nums = [int(s) for s in input().strip().split()]
target = len(nums)
accs = sorted((v % target, i) for (i, v) in enumerate(accumulate(nums, initial=0)))
(lo, hi) = (0, 1)
(lo_acc, lo_count) = (accs[0][0], 1)
def inc_lo():
global lo, lo_acc, lo_count
lo += 1
# TODO: do we need to reprocess lo_acc and lo_count always lol
if lo_acc == accs[lo][0]:
lo_count += 1
else:
lo_acc = accs[lo][0]
lo_count = 1
solution = 0
while hi < len(accs):
v = accs[hi][0] - accs[lo][0]
if (v < 0) or (lo == hi):
hi += 1
elif v > 0:
inc_lo()
elif (accs[lo + 1][0] == lo_acc) and (accs[lo + 1][1] < accs[hi][1]):
inc_lo()
else:
if accs[lo][1] < accs[hi][1]:
solution += lo_count
hi += 1
print(solution)The only differences are that I calculated the modulos when constructing accs:
target = len(nums)
accs = sorted((v % target, i) for (i, v) in enumerate(accumulate(nums, initial=0)))and I changed the conditions in the main loop to v < 0 and v > 0.
Subarray Distinct Values [Spec] (2024-02-15)
Very straightforward sliding window strategy:
#!/usr/bin/env python3
from collections import Counter
(_, k) = [int(s) for s in input().strip().split()]
nums = [int(s) for s in input().strip().split()]
(lo, hi) = (0, 0)
cnt = Counter(nums[:1])
solution = 0
while hi < len(nums):
if len(cnt) <= k:
solution += hi - lo + 1
hi += 1
if hi < len(nums):
cnt[nums[hi]] += 1
else:
if cnt[nums[lo]] == 1:
del cnt[nums[lo]]
else:
cnt[nums[lo]] -= 1
lo += 1
print(solution)